Calculate Probability Of Slot Machine
- Probability with slot machines, statistics? Let's say there's a typical slot machine. It has 3 wheels, each are marked with 20 symbols (equal spacing around the wheels) Each wheel spins independantly from one another. Wheel 1 has - 2 stars Wheel 2 has - 10 stars Wheel 3 has - 3 stars 2 stars?
- To calculate the total number of combinations of symbols on this machine, we multiple the number of stops (symbols) on each reel by the number of stops on each of the remaining reels. For a three reel machine with twenty stops per reel, we have 20 x 20 x 20 = 8,000 combinations of slot symbols.
This eighth book of the author on gambling math presents in accessible terms the cold mathematics behind the sparkling slot machines, either physical or virtual. It contains all the mathematical facts grounding the configuration, functionality, outcome, and profits of the slot games.
You want to know how to calculate probability in gambling?
The first step is understanding what the word means.
The word probability has 2 meanings:
- The likelihood that something will or won’t happen.
- The branch of mathematics that measures that likelihood.
If you’re a casual gambler, you might have a vague idea that the probability of a win can be measured.
But until you understand the specifics of how to calculate probability, you can’t be considered a sophisticated gambler.
This post explains how to calculate probability in gambling and why it matters to gamblers.
How to Calculate Probability as a Fraction
Whether something will happen can be measured on a scale from 0 to 1. If something can never happen, its probability is 0.
Here’s an example of something with a 0 probability:
You have a standard 6-sided die. It’s numbered from 1 to 6. The probability of rolling a 7 is 0. It’s not possible.
Here’s an example of something with a probability of 1:
You have a trick coin with 2 heads. When you flip the coin, the probability of it landing on heads is 1. (And the probability of it landing on tails is 0.)
Most events have a degree of uncertainty to them, though. You can measure how often you expect those events to happen as a fraction.
Here’s an example:
You flip a normal coin with a heads side and a tails side. The probability of getting heads is 1/2.
The Magic Formula for Calculating a Probability
The formula for calculating that probability is simplicity itself:
You divide the number of ways you can achieve the desired event by the total number of possible events.
In the case of a coin toss, there’s only one way to get heads. But there are 2 possible results.
1 divided by 2 is 1/2.
This probability can be expressed in any of the following ways:
- As a fraction.
- As a decimal.
- As a percentage.
- As odds.
Some of these are more useful than others in certain situations. I’ll get into that a little more later in this post.
But for now, let’s convert that 1/2 probability of getting heads into each of those 4 ways:
- As a fraction, the probability is represented as 1/2.
- As a decimal, the probability is represented as 0.5.
- As a percentage, the probability is represented as 50%.
- As odds, the probability is represented as 1 to 1.
Most of us are familiar with probability represented as a percentage. After all, most people watch the nightly news or at least look at the Internet for the weather report.
And they always express the probability of rain with a percentage.
If there’s a 20% chance of thunderstorms, we know that there’s a roughly 1 in 5 chance of rain, thunder, and lightning.
Bigger Probability Problems
Probability gets more interesting as you start calculating probabilities for multiple events.
Let’s say you want to know the probability of getting heads twice in a row.
This is an example of an “and” probability. You need to get heads on the first throw AND on the second throw to win this bet.
When calculating a probability for multiple events that use the word “and”, you multiply the probability of event 1 by the probability of event 2.
In this case, that can be represented as 1/2 X 1/2 = 1/4.
The probability of getting heads twice in a row is, therefore, 1/4, which can also be expressed as 25%.
Notice that the probability is lower. That’s what happens when you multiply fractions.
Let’s say you want to calculate an “OR” probability instead. This time, let’s use a 6-sided die as an example.
You want to know the probability of rolling a 6 on at least one of 2 rolls.
That’s an example of an “or” probability. You want to know how likely it is that you’ll roll a 6 on the first roll OR on the second roll.
You have 6 possible results, but only 1 of them is the 6. So your probability of rolling a 6 on either roll is 1/6.
In an “or” probability, you add the probabilities together. In this case, that would be represented as 1/6 + 1/6 = 2/6. Of course, most people would reduce 2/6 to 1/3, which is also often expressed as a percentage, 33.33%.
Expressing Probabilities as Odds
The tricky expression of this isn’t as a fraction, a decimal, or a percentage. Most of us are familiar with these expressions. That’s basic math.
But most of us don’t have backgrounds in statistics, so we’re not used to expressing probabilities in odds format.
Here’s how to calculate probability in odds format.
When expressing a probability as odds, you just compare the number of ways something can’t happen with the number of ways it can happen.
If you want to look at the odds of rolling a 6 on a single 6-sided die, you’d look at the number of ways you could possibly roll anything else versus the number of ways you can roll the 6.
In this case, you’re looking at 5 to 1. You have 5 ways to roll anything but a 6, and only one way to roll a 6.
This becomes useful when you start looking at the expected profit or loss on a bet.
Bets always pay off at certain odds–how much you win versus how much you risk.
Many bets pay off at 1 to 1, or even odds. This is especially true of bets you make in a casual situation.
Here’s an example:
You’re shooting pool at your local bar, and you bet your buddy $20 on the next game. If you win, he gives you $20. If he wins, you give him $20.
But let’s suppose that your levels of skill are different.
Let’s suppose that he’s better than you, and he stands to win 2 out of 3 times.
The odds of him winning are 2 to 1.
If the bet pays off at even odds, in the long run, he’ll profit from playing pool against you under those terms.
He’ll win, on average, $40 during 3 games. You’ll win $20. His net win is $20.
Average that net win out over the 3 games, and he’s winning $6.67 per game on average.
If this were a casino game, you could translate that into a percentage, and you’d have the house edge.
But I’m going to write another post about the house edge, soon. And I don’t want to spoil it for you.
Instead, I’m going to leave you with one more example of how odds are used–this time in a game of poker.
In this example, we’re going to assume that you have 4 cards to a flush, and you’re reasonably sure you’ll win the hand if you make the flush. You’re playing Texas holdem, and you have 2 cards that are hearts in your hand, and there are 2 hearts on the flop.
You have 2 cards yet to come.
You might think that the probability of getting a heart on the next card is 1/4. After all, there are only 4 possible suits in a deck of cards.
But that doesn’t take into account the cards that have already been dealt.
You have 2 cards, and there are 3 cards on the board. So there are only 47 cards left.
The deck has a total of 13 hearts in it, but you know that 4 of them are already gone, leaving 9 hearts.
The probability of being dealt a heart for your next card is 9/47.
If you don’t get a card on the next hand, you get another chance, and this time, the probability is 9/46.
The easiest thing to do here is convert those into percentages first.
You have a 19% chance of getting a heart on the turn. You then have another 19% chance, more or less, of getting a heart on the river.
Add those together, and you get 38%. That’s close to 38%, or around 3 to 1.
If it costs $100 to get into the pot, you stand to make a profit if the pot has more than $300 in it. If it has less than $300 in it, you stand to lose money over time.
Finally
These are just some rough probability examples. But this is the first step in becoming a savvy gambler–knowing how to calculate probability.
Being able to compare the odds of winning with the odds you’re getting paid enables you to decide whether a bet is profitable.

Not long ago, I wrote about the skills you need to master video poker. Learning how to calculate probability in gambling is included as one of those skills.
Tomorrow I’ll write more about the house edge in casino games.
First of all, we must start with the number of possible combinations. In the case of slots, it is relatively simple – just multiply the numbers of symbols on each reel. The oldest slots had, for example, 3 reels with ten different symbols on each. The total number of combinations that could appear on the panel was 1,000 (10 x 10 x 10).
The number of combinations in today’s slots is somewhat higher. If we assume five reels with 30 symbols on each, we get a total of 243,000,000 combinations.
If you want to calculate your chances to win on an online slot machine, all you need is this simple equation:
Number of winning combinations / Total number of combinations
To calculate the payout of the slot machine, modify the formula a little:
Σ (winning combination_k * possible yield_k) / (Total number of combinations)
Let’s analyze a few basic slot machines. For the purposes of our article and in order to simplify the calculation, we will assume that the slot machine has only one payout line and the bet is one coin per round.
Analysis of the simplest slot machine
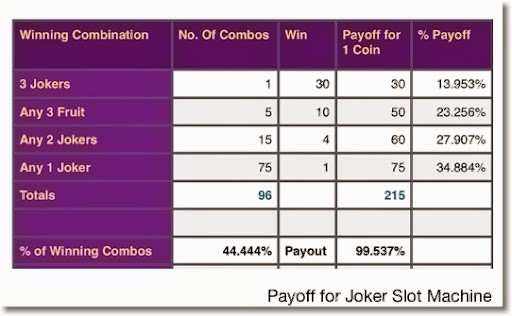
Let’s go back to the past and assume that the machine only has 3 reels and there is an apple, an orange, a lemon, a banana, a melon and a joker symbol on each. The individual combinations produce these winnings:
- Three jokers win 30 coins
- Any three fruits win 10 coins
- Two jokers win 4 coins
- One joker wins 1 coin
The total number of combinations is 216 (6 x 6 x 6).
Total number of winning combinations:
- In the first case there is only one winning combination (1 x 1 x 1 = 1)
- In the second case we have 5 winning combinations (3 times apple or 3 times orange or 3 times lemon, …) (1 x 1 x 1) x 5 = 5
- The joker may appear on any two reels. The calculation is as follows: 1 x 1 x 5 + 1 x 5 x 1 + 5 x 1 x 1 = 15
- The joker may appear on any reel. 1 × 5 × 5 + 5 × 1 × 5 + 5 × 5 × 1 = 75
Our simplified model thus contains 1 + 5 + 15 + 75 = 96 winning combinations. The table below shows the probability of a payout.
| Winning combination | Number of combinations | Winning | Returns for 1 coin | Chance to win |
| 3 jokers | 1 | 30 | 30 | 13.953% |
| Any fruit | 5 | 10 | 50 | 23.256% |
| 2 jokers | 15 | 4 | 60 | 27.907% |
| 1 joker | 75 | 1 | 75 | 34.884% |
| Total | 96 | 215 | ||
| % for the winning combination | 44.444% | Payouts | 99.537% |
Calculation of payouts according to the formula
Σ (winning combination_k * possible yield_k) / (Total number of combinations)
(1 × 30 + 5 × 50 + 15 × 4 + 75 × 1)/(6 × 6 × 6) = 215/216 ≈ 0.99537
In this case, the slot machine has a payout ratio of 99.53%, which is very nice, but in a real casino, you will not find the same results. The average returns of slots online casinos will be between 94% and 98%.
The table also clearly shows how single coin wins affect payouts. If the win of each combination were equal to one coin, the winning ratio would drop to 44.4%. And that’s a very small number.
Analysis of a more complicated slot

Because the previous example was too distant from reality, let’s show you another example with higher numbers. To simplify, let’s assume again that there is only one payline, the slot machine has 3 reels and a total of 6 symbols that can appear on the panel:
| Symbol | Reel 1 | Reel 2 | Reel 3 |
| BAR | 1 | 1 | 1 |
| SEVEN | 3 | 1 | 1 |
| Cherry | 4 | 3 | 3 |
| Orange | 5 | 6 | 6 |
| Banana | 5 | 6 | 6 |
| Lemon | 5 | 6 | 6 |
| Total | 23 | 23 | 23 |
The total number of combinations is 23 x 23 x 23 = 12,167.
Winning combinations with single coin returns:
- 3x BAR, win 60 coins, number of combinations 1
- 3x SEVEN, win 40 coins, number of combinations 3 x 1 x 1 = 3
- 3x Cherry, win 20 coins, number of combinations 4 x 3 x 3 = 36
- 3x Other fruit, win 10 coins, number of combinations (5 x 6 x 6) x 3 = 540
- Cherry on two reels, win 4 coins, number of combinations 651
- Cherry on one reel, win 1 coin, number of winning combinations 3,880
Calculation for no. 5:
Cherry, Cherry, Other: 4 x 3 x (23 – 3) = 240
Cherry, Other, Cherry: 4 x (23 – 3) x 3 = 240
Other, Cherry, Cherry: (23 – 4) x 3 x 3 = 171
Calculation for no. 6:
First reel: 4 x 20 x 20 = 1,600
Second reel 19 x 3 x 20 = 1,120
Third reel 19 x 20 x 3 = 1,120
Calculate Probability Of Slot Machines
The following table shows the amount of payout and the chance of winning for the individual combinations.
Calculate Probability Of Slot Machines
| Winning combination | Number of combinations | Winning | Returns for 1 coin | Chance to win |
| 3x BAR | 1 | 60 | 60 | 0.495% |
| 3x SEVEN | 3 | 40 | 120 | 0.989% |
| 3x Cherry | 36 | 20 | 720 | 5.934% |
| 3x Other fruit | 540 | 10 | 5,400 | 44.507% |
| 2x Cherry | 651 | 3 | 1,935 | 16.097% |
| 1x Cherry | 3,880 | 1 | 3,880 | 31.979% |
| Total | 5,111 | 12,133 | ||
| % of winning combinations | 42.007% | Payout | 99.721% |
As you can see, the payout ratio is very high again at 99.721% (12,133 / 12,161). If the slot were to pay a straight win for each winning combination in the amount of 1 coin, the payout ratio would be down to 42,007%.